https://www.acmicpc.net/problem/13512
13512번: 트리와 쿼리 3
N개의 정점으로 이루어진 트리(무방향 사이클이 없는 연결 그래프)가 있다. 정점은 1번부터 N번까지 번호가 매겨져 있고, 간선은 1번부터 N-1번까지 번호가 매겨져 있다. 가장 처음에 모든 정점의
www.acmicpc.net
Heavy-Light Decomposition
일단 트쿼 3을 풀기 전에, LCA 2를 HLD를 이용해서 풀어보자.
1. dfs를 통하여 한 노드를 루트로 하는 서브트리의 크기를 저장해둔다.
|
1
2
3
4
5
6
7
|
def dfs(x, p):
par[x] = p
sz[x] = 1
for i in g[x]:
if i != p:
sz[i] += dfs(i, x)
return sz[x]
|
cs |
x는 현재 노드, p는 부모 노드이다.
par은 정점의 부모 노드, sz는 서브트리의 크기가 담긴 배열이다.
2. dfs를 또 돌린다. 이번에는, 서브트리가 큰 쪽을 향해 우선적으로 내려가며 체인을 만든다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
def hld(x, p, num, depth):
d[x] = depth
chIdx[x] = len(ch[num])
chNum[x] = num
ch[num].append(x)
go = -1
for i in g[x]:
if go == -1 or sz[i] > sz[go]:
if i != p:
go = i
if go != -1:
hld(go, x, num, depth)
for i in g[x]:
if i != go and i != p:
hld(i, x, i, depth + 1)
|
cs |
x는 현재 노드, p는 부모 노드, num은 체인의 번호, depth는 체인의 깊이이다.
d는 트리 내 체인의 깊이이다. 노드의 깊이가 아니다.
ch는 체인의 정보(?)이고, ch[x]에는 x번째 체인의 노드들이 담기게 된다.
chIdx는 노드의 체인 내 인덱스, chNum은 체인의 꼭대기 노드가 담긴 배열이다.
go는 무거운 노드의 번호이고, 만약 더 내려갈 수 있는 노드가 존재하지 않는다면 go는 갱신이 되지 않아 -1일 것이다.

이렇게 생긴 트리가 있다고 하자. 이 트리는 1, 2번 과정을 거치면,

그림처럼 같은 색끼리 체인을 형성하게 된다.
3. LCA를 찾는다.
|
1
2
3
4
5
6
7
|
def getLca(x, y):
while chNum[x] != chNum[y]:
if d[x] > d[y]:
x = par[chNum[x]]
else:
y = par[chNum[y]]
return x if chIdx[x] < chIdx[y] else y
|
cs |
같은 깊이의 노드들은 같은 체인에 들어가지 않는다는 성질 때문에,
두 노드가 같은 체인에 속한다면 둘은 부모/자식 관계임을 알 수 있다.

따라서 두 노드가 속한 체인이 다르다면, 체인이 같아질 때까지 깊은 쪽 체인에 속하는 노드를 올려주면 된다.
두 체인의 깊이가 같지만 서로 다른 체인이라면, 아무거나 올린다.
두 노드가 속한 체인이 같아지면, 위에 있는 노드가, 즉 체인 내 인덱스가 작은 노드가 LCA이다.
이를 모두 합친 코드이다.
템플릿 코드는 아래쪽에 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
sys.setrecursionlimit(10**5)
g = [[] for _ in range(101010)]
sz = [0 for _ in range(101010)]
par = [0 for _ in range(101010)]
def dfs(x, p):
par[x] = p
sz[x] = 1
for i in g[x]:
if i != p:
sz[i] += dfs(i, x)
return sz[x]
ch = [[] for _ in range(101010)]
d = [0 for _ in range(101010)]
chNum = [0 for _ in range(101010)]
chIdx = [0 for _ in range(101010)]
def hld(x, p, num, depth):
d[x] = depth
chIdx[x] = len(ch[num])
chNum[x] = num
ch[num].append(x)
go = -1
for i in g[x]:
if go == -1 or sz[i] > sz[go]:
if i != p:
go = i
if go != -1:
hld(go, x, num, depth)
for i in g[x]:
if i != go and i != p:
hld(i, x, i, depth + 1)
def getLca(x, y):
while chNum[x] != chNum[y]:
if d[x] > d[y]:
x = par[chNum[x]]
else:
y = par[chNum[y]]
return x if chIdx[x] < chIdx[y] else y
n = ip()
for nodes in range(n - 1):
i, j = mip()
g[i].append(j)
g[j].append(i)
dfs(1, 0)
hld(1, 0, 1, 0)
m = ip()
for query in range(m):
i, j = mip()
print(getLca(i, j))
|
cs |

잘 돌아간다.
이제 트쿼 3을 풀어보자. 앞서 LCA 2를 풀 때와 비슷하게(?) 풀면 된다.
1. dfs를 돌며 서브트리의 크기를 기록한다. 깊이는 기록할 필요가 없어졌다.
그리고, 두 번째 dfs에서는 방문 순서대로 정점에 번호를 부여하며 hld를 진행한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
def dfs(x):
sz[x] = 1
for i in g[x]:
if sz[i] == 0:
par[i] = x
dfs(i)
sz[x] += sz[i]
index = 0
def hld(x):
global index
heavy = -1
index += 1
idx[x] = index
ridx[idx[x]] = x
for i in g[x]:
if heavy == -1 or sz[i] > sz[heavy]:
if par[i] == x: # Same chain
heavy = i
if heavy != -1:
ch[heavy] = ch[x]
hld(heavy)
for i in g[x]:
if par[i] == x and i != heavy: # Create new chain
ch[i] = i
hld(i)
|
cs |
변수가 살짝 바뀌었다
2. 검은색 정점을 찾기 위해, 최솟값 세그먼트 트리를 만든다.
트리에서 정점 u에서 정점 v로 가는 단순 경로는 유일하므로, 정점 1에서 어떤 정점 x로 가는 길에 나오는 검은색 정점들 중 먼저 만나는 정점의 번호는 가장 작은 번호가 된다. dfs ordering은 이것 때문에 사용했다.
흰색 정점은 INF, 검은색 정점은 새로 부여한 정점의 번호로 세그먼트 트리에 넣는다.
간단하니 코드는 생략한다.
3. 열심히 구현한다.
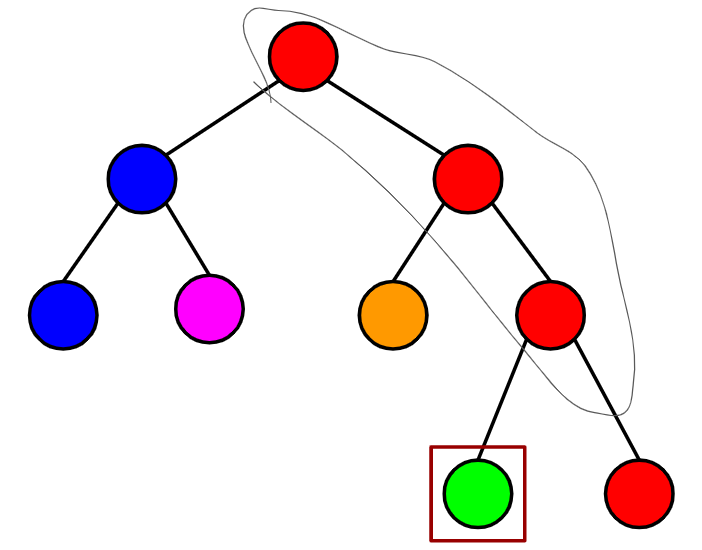
네모 친 정점부터 위쪽으로 올라가면서 답을 갱신해가면 된다.
이때 같은 체인에 들어있는 정점들은 연속적인 번호로 이루어져 있기 때문에, O(X)가 아닌 O(lgX)의 시간으로 올라갈 수 있다. X는 경로 상에서 같은 체인에 속하는 정점의 개수이다.(그림에서는 X=3)
Update는 쉽다. xor로 색 정보를 알 수 있다.
전체 코드는 다음과 같다.
템플릿 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
|
import sys, math
import heapq
from collections import deque
input = sys.stdin.readline
hqp = heapq.heappop
hqs = heapq.heappush
#input
def ip(): return int(input())
def sp(): return str(input().rstrip())
def mip(): return map(int, input().split())
def msp(): return map(str, input().split().rstrip())
def lmip(): return list(map(int, input().split()))
def lmsp(): return list(map(str, input().split().rstrip()))
#gcd, lcm
def gcd(x, y):
while y:
x, y = y, x % y
return x
def lcm(x, y):
return x * y // gcd(x, y)
#prime
def isPrime(x):
if x<=1: return False
for i in range(2, int(x**0.5)+1):
if x%i==0:
return False
return True
# Union Find
# p = {i:i for i in range(1, n+1)}
def find(x):
if x == p[x]:
return x
q = find(p[x])
p[x] = q
return q
def union(x, y):
x = find(x)
y = find(y)
if x != y:
p[y] = x
def getPow(a, x):
ret = 1
while x:
if x&1:
ret = (ret * a) % MOD
a = (a * a) % MOD
x>>=1
return ret
def getInv(x):
return getPow(x, MOD-2)
|
cs |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
|
sys.setrecursionlimit(10**5)
INF = int(1e9)
seg = [0 for _ in range(404040)]
g = [[] for _ in range(101010)]
par = [0 for _ in range(101010)]
sz = [0 for _ in range(101010)]
c = [0 for _ in range(101010)]
idx = [0 for _ in range(101010)]
ridx = [0 for _ in range(101010)]
ch = [0 for _ in range(101010)]
def update(x, s, e, idx, v):
if idx < s or e < idx:
return
if s != e:
m = (s + e) // 2
update(x * 2, s, m, idx, v)
update(x * 2 + 1, m + 1, e, idx, v)
seg[x] = min(seg[x * 2], seg[x * 2 + 1])
return
seg[x] = v
def getMin(x, l, r, s, e):
if e < l or r < s:
return INF
if l <= s and e <= r:
return seg[x]
m = (s + e) // 2
return min(getMin(x * 2, l, r, s, m), getMin(x * 2 + 1, l, r, m + 1, e))
def dfs(x):
sz[x] = 1
for i in g[x]:
if sz[i] == 0:
par[i] = x
dfs(i)
sz[x] += sz[i]
index = 0
def hld(x):
global index
heavy = -1
index += 1
idx[x] = index
ridx[idx[x]] = x
for i in g[x]:
if heavy == -1 or sz[i] > sz[heavy]:
if par[i] == x: # Same chain
heavy = i
if heavy != -1:
ch[heavy] = ch[x]
hld(heavy)
for i in g[x]:
if par[i] == x and i != heavy: # Create new chain
ch[i] = i
hld(i)
def getAns(x):
ret = INF
while ch[1] != ch[x]:
ret = min(ret, getMin(1, idx[ch[x]], idx[x], 1, n))
x = par[ch[x]]
ret = min(ret, getMin(1, idx[ch[x]], idx[x], 1, n))
return ret
n = ip()
for nodes in range(n - 1):
i, j = mip()
g[i].append(j)
g[j].append(i)
ch[1] = 1
dfs(1)
hld(1)
for i in range(1, n + 1):
update(1, 1, n, idx[i], INF)
qr = ip()
for query in range(qr):
i, j = mip()
if i == 1:
c[j] ^= 1
update(1, 1, n, idx[j], idx[j] if c[j] else INF)
else:
ans = getAns(j)
print(ridx[ans] if ans != INF else -1)
|
cs |

Python3에서는 재귀 제한을 10**6으로 설정해야된다. 왜지
'백준 문제풀이' 카테고리의 다른 글
| 백준 20052 - 괄호 문자열 ? [Python] (0) | 2022.04.09 |
|---|---|
| 백준 21908 - Disk Sort [Python] (0) | 2022.03.24 |
| 백준 3056 - 007 [Python] (0) | 2021.09.02 |
| 백준 1311 - 할 일 정하기 1 [Python] (0) | 2021.09.02 |
| 백준 22040 - 사이클 게임 [Python] (0) | 2021.09.02 |