https://www.acmicpc.net/problem/26104
26104번: Empty Quadrilaterals
Your program is to read from standard input. The input starts with a line containing an integer $n$ ($1 ≤ n ≤ 300$), where $n$ denotes the number of points in the set $P$. In the following $n$ lines, each line consists of two integers, ranging from $-1
www.acmicpc.net
대회 당시 못 풀어서 한이 맺힌 문제다. 너무 화나서 대회가 끝난 이후로 계속 고민해서 풀었다.
어떤 다각형 내부의 어떤 점도 존재하지 않을 때, 이 다각형을 좋은 다각형이라고 하자. 일단 좋은 사각형 대신, 좋은 삼각형의 개수를 구해보자. 한 점 \(A\) 를 고정하고, 이 점을 기준으로 360도 정렬을 한다. 그리고 다른 점 \(B\) 를 고정하자. 이 점에서부터 반시계 방향으로 돌면서 점 \(B\), \(C\), \(now\) 의 ccw를 확인한다. 점 \(C\) 는 지금까지 봤던 점들 중 가장 반시계방향에 위치한 점이다.

위 그림처럼 점 \(B\), \(C\), \(now\) 가 시계방향으로 위치한다면, 점 \(A\), \(B\), \(now\) 를 꼭짓점으로 갖는 삼각형 내부에 점이 존재한다. 삼각형 버전은 시간복잡도 \(O(N^3)\) 에 해결할 수 있다. 참고로 삼각형 버전 문제는 작년 인터넷 예선에 나왔다.
이제 사각형의 경우를 해결해야 한다. 먼저 점 \(A\), \(B\) 를 고정하고, 이 두 점을 잇는 선분을 사각형의 대각선으로 보자. 이 선분 양 쪽 방향 각각에 대하여 좋은 삼각형의 개수를 센 다음, 이 둘을 곱하면 된다. 사각형 내부에 들어가는 대각선의 개수는 볼록 사각형의 경우는 \(2\), 오목 사각형의 경우는 \(1\)이다. 좋은 볼록 사각형의 개수를 \(x\), 좋은 오목 사각형의 개수를 \(y\) 라고 하자. 우리는 \(2x + y\) 의 값을 위 방법으로 구했다.
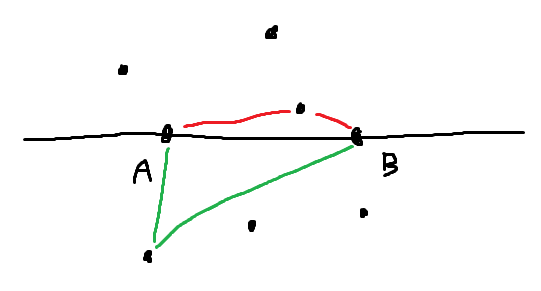
그러나 우리가 원하는 답은 \(x + y\) 이다. 오목 사각형의 개수 \(y\) 를 구해보자. 한 쪽에서 삼각형의 끝 점 \(L\) 을 고정했다면, 반대쪽에서 점 \(R\) 을 옮김에 따라 사각형은 오목 -> 볼록 -> 오목 으로 변화한다. 이를 이용해 각 \(LBR\) 또는 \(LAR\) 이 180도를 넘어가도록 하는 점들을 찾을 수 있다. 각의 중심이 될 수 있는 점 \(A\), \(B\) 각각을 기준으로 정렬을 따로 해야 한다. 이분 탐색, 투 포인터 등의 방법으로 찾을 수 있다. 각 \(LBR\) 와 \(LAR\) 각각에 대해 개수를 찾으면 된다.
주의할 점이 하나 있다. \(y\)를 구할 때, 삼각형 \(ABC\) 가 좋은 삼각형이 되도록 하는 점 \(C\) 의 후보군에서만 확인해야 한다. 따라서 나쁜 삼각형이 되는 점들은 모두 제거한 채로 구해야 한다. 이 값도 답에 더해주는 것으로, \(2x + 2y\) 를 구할 수 있다.

위 과정을 쭉 시행한 후, 답을 \(4\)로 나눠주면 된다. 전체 시간복잡도는 \(O(N^3lgN)\) 이다. 상수가 커지면 가차없이 TLE를 받는다. 나는 상수를 더 줄이기 귀찮아서 최후의 발악으로 Clang으로 내봤는데 맞았다. 문제의 정답률을 낮춘 주범이 되었다. 정답 코드는 다음과 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
|
#include <bits/stdc++.h>
#define all(v) v.begin(),v.end()
using namespace std;
using ll = long long;
using ld = long double;
typedef pair<ll, ll> pll;
typedef pair<int, int> pii;
typedef pair<int, ll> pil;
#define X first
#define Y second
#define endl '\n'
pll a[301];
pll O = {0, 0};
bool ccw(pll p1, pll p2, pll p3){
ll ret = p1.X * p2.Y + p2.X * p3.Y + p3.X * p1.Y - p1.Y * p2.X - p2.Y * p3.X - p3.Y * p1.X;
return ret > 0;
}
bool cmp(pll l, pll r){
l.X -= O.X; l.Y -= O.Y;
r.X -= O.X; r.Y -= O.Y;
if ((l.X < 0) != (r.X < 0)){
return l.X < r.X;
}
return l.Y * r.X < l.X * r.Y;
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(nullptr);
int n; cin >> n;
for (int i=0;i<n;i++){
cin>>a[i].X>>a[i].Y;
}
ll ans = 0;
if (n < 4) {
cout << 0 << endl;
return 0;
}
for (int i=0;i<n;i++){
O = a[i];
vector<pll> v;
for (int j=0;j<n;j++){
if (a[i] == a[j]) continue;
v.emplace_back(a[j]);
}
sort(v.begin(), v.end(), cmp);
for (int j=0;j<n-1;j++){
vector<pll> up, dw, cup, cdw;
for (int k=j;k<j+n-1;k++){
if (v[j] == v[k % (n - 1)]) continue;
if (ccw(a[i], v[j], v[k % (n - 1)])) up.emplace_back(v[k % (n - 1)]);
else dw.emplace_back(v[k % (n - 1)]);
}
if (up.empty() || dw.empty()) continue;
ll L = 0, R = 0;
pll pt;
L = 1;
pt = up[0];
cup.emplace_back(pt);
for (ll k=1;k<up.size();k++){
if (!ccw(v[j], pt, up[k])) continue;
else {
L += 1;
pt = up[k];
cup.emplace_back(pt);
}
}
R = 1;
pt = dw[dw.size() - 1];
cdw.emplace_back(pt);
for (ll k=dw.size()-2;k>=0;k--){
if (ccw(v[j], pt, dw[k])) continue;
else {
R += 1;
pt = dw[k];
cdw.emplace_back(pt);
}
}
reverse(cdw.begin(), cdw.end());
up.clear(); dw.clear();
ll now = 0;
int r = cdw.size() - 1;
for (int l=cup.size()-1;l>=0;l--){
while (r >= 0 && ccw(cup[l], a[i], cdw[r])) r--;
now += r + 1;
}
cup.emplace_back(a[i]);
cdw.emplace_back(a[i]);
O = v[j];
sort(cup.begin(), cup.end(), cmp);
sort(cdw.begin(), cdw.end(), cmp);
int s = 0;
for (int k=0;k<cup.size();k++){
if (cup[k] == a[i]) {
s = k; break;
}
}
for (int k=s;k<s+cup.size();k++){
if (cup[k%cup.size()] == a[i]) continue;
up.emplace_back(cup[k%cup.size()]);
}
for (int k=0;k<cdw.size();k++){
if (cdw[k] == a[i]) {
s = k; break;
}
}
for (int k=s;k<s+cdw.size();k++){
if (cdw[k%cdw.size()] == a[i]) continue;
dw.emplace_back(cdw[k%cdw.size()]);
}
r = 0;
for (auto & l : up){
while (r < dw.size() && !ccw(l, v[j], dw[r])) r++;
now += dw.size() - r;
}
ans += now + L * R;
}
}
cout << ans / 4 << endl;
return 0;
}
|
cs |
'백준 문제풀이' 카테고리의 다른 글
| 백준 1376 - 민식우선탐색 (0) | 2022.12.15 |
|---|---|
| 백준 23750 - Leader-based Team Distribution (2) | 2022.12.12 |
| 백준 20306 - 블랙홀 (1) | 2022.11.12 |
| 백준 18619 - Alakazam (0) | 2022.10.29 |
| 백준 18032 - Dazzling Stars (0) | 2022.10.17 |